Teoría de grupos
A teoría de grupos ye a branca de l'alchebra que estudeya os grupos. Un grupo ye una estructura alchebraica que consta d'un conchunto que ye definito chunto con una operación que combina cualsiquier parella d'os suyos elementos ta formar un tercer elemento. Debito a que se pueden calificar como un grupo, o conchunto y operación han de satisfer unas cuantas condicions ditas axiomas de grupo, istas condicions son: tener a propiedat asociativa, tener elemento identidat y elemento inverso. Mientres que istas caracteristicas son familiars a muitas estructuras matematicas, como os diferents sistemas de numeros (por eixemplo os enters dotatos d'a operación d'adición forman una estructura de grupo) a formulación d'os axiomas se desepara d'a naturaleza concreta d'o grupo y o suyo funcionamiento. Ixo permite, en alchebra abstracta y altros campos, maniar entidaz d'orichens matematicos muit diferents d'una manera flexible, mientres se conservan aspectos estructurals esencials de muitos obchectos. A utilidat d'os grupos en numerosas arias (tanto adintro como difuera d'as matematicas) fa d'éls un prencipio central arredol d'o cual s'organizan as matematicas contemporanias.[1][2]
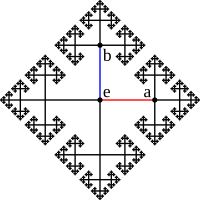

Os grupos tienen una relación muit estreita con a noción de simetría. Un grupo de simetría codifica as caracteristicas de simetría d'un obchecto cheometrico: consiste en o conchunto de transformacions que dixan inalterato l'obchecto, y a operación de combinar dos d'istas transformacions realizando-ne una dimpués de l'atra. Istos grupos de simetría, mas que mas os grupos de Lie continos, chugan un papel important en muitas disciplinas academicas. Os grupos de matrices, por eixemplo, se pueden fer servir ta entender as leis fisicas fundamentals en que se basan a relatividat y os fenomenos de simetria en a quimica molecular.
O concepto d'un grupo apareixió con o estudio d'as ecuacions polinomicas, prencipiato por Évariste Galois mientres os anyos 1830. Dimpués de contribucions dende atros campos como a teoría de numeros y a cheometría, la noción de grupo se cheneralizó y s'establió ta cutio arredol de 1870. A moderna teoría de grupos (una disciplina matematica muit activa) estudeya os grupos per se.[3] Ta esplorar os grupos, os matematicos han ideyato diversas nocions como dividir os grupos en trozos mas chicoz y mas comprensibles, como los subgrupos, grupos cocients y grupos simples. Amás d'as suyas propiedaz abstractas, os teoricos d'os grupos tamién estudeyan as formas diferents en que un grupo se puet exprisar en forma concreta (as suyas representacions de grupo), tanto dende un punto d'envista teorico como d'un punto d'envista computacional. Una teoría muit rica s'ha desembolicato ta os grupos finitos, que remató con a clasificación d'os grupos simples finitos rematata en 1983.
Definición y ilustración
editarUn primer eixemplo: os enters
editarUn d'os grupos mas familiars ye o conchunto d'os numeros enters Z que consiste en os numeros
- ..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...[4]
As propiedaz siguients de l'adición d'enters sirven como modelo ta os axiomas de grupo abstractos que se dan en definición mas entabant.
- Ta cualsiquier parella d'enters a y b, a suma a + b ye tamién un entero. En atras parolas, o proceso d'adición d'enters nunca no puet producir un resultato que no sía un entero. Ista propiedat se conoixe como clausura respecto de l'adición.
- Ta toz os enters a, b y c, (a + b) + c = a + (b + c). Exprisato en parolas, sumando primero a y b, y dimpués sumando lo resultato con c da o mesmo resultato final que sumando a a lo resultato de sumar b y c, ista propiedat se conoixe como propiedat asociativa.
- Si a ye un entero cualsiquiera, allora 0 + a = a + 0 = a. D'o cero se'n diz que ye o elemento neutro u identidat de l'adición porque en sumar-lo a cualsiquier entero da o mesmo entero.
- Ta cada entero a, bi ha un entero b tal que a + b = b + a = 0. O entero b se diz elemento inverso u simetrico d'o entero a y se denota −a.
Introducción
editarOs enters, chunto con a operación "+", forman un ochecto matematico que perteneixe a una clase ampla en la que bi ha atros obchectos que comparten aspectos estructurals similars. Ta entender bien istas estructuras sin tratar con cada caso concreto deseparato, se desarrolla la definición abstracta siguient que incluye l'eixemplo citato chunto con muitos atros, un d'os cuals ye o grupo de simetría que se detalla mas entabant
Un grupo ye un conchunto, G, chunto con una operación binaria "•" que combina dos elementos cualsiquiera a y b de G ta formar unatro elemento denotato a • b. O simbolo "•" ye un elemento cheneral ta representar una operación cualsiquiera, como l'adición en l'eixemplo anterior. Ta poder-se calificar como un grupo, lo conchunto y a operación (G, •), han de satisfer cuatre requisitos conoixitos como los axiomas de grupo:[5]
1. Clausura. Ta tot a, b de G, o resultato d'a operación a • b tamién perteneixe a G.[6] 2. Propietat asociativa. Ta toz a, b y c de G, se cumple a ecuación (a • b) • c = a • (b • c). 3. Elemento identidat. Existe un elemento e de G, tal que ta toz os elementos a de G, se cumple a ecuación y • a = a • y = a. 4. Elemento inverso. Per a tot a de G, existe un elemento b de G tal que a • b = b • a = y, a on que y ye l'elemento identidat.
L'orden en que se fa la operación de grupo puet estar significativo. En atras parolas, o resultato d'operar o elemento a con o elemento b no tien por qué dar o mesmo resultato que operando b con a; a ecuación
- a • b = b • a
puet no estar siempre cierta. Ista ecuación siempre se cumple en o grupo d'enters con l'adición, porque a + b = b + a ta dos enters cualsiquiera (propiedat commutativa de l'adición). Manimenos, no se cumple siempre en o grupo de simetria que apareixe en l'eixemplo de mas entabant. Os grupos ta os que a ecuación a • b = b • a se cumple siempre se dicen abelians (en honor a Niels Abel). Asinas, o grupo d'os enters con l'adición ye abelián, pero lo grupo de simetría siguient no'n ye.
Definición de grupo
editarUn grupo ye un conchunto G en o que s'ha definito una lei de composición interna que satisfa os siguients axiomas:
Por tanto, un grupo ye formato por un conchunto d'obchectos abstractos u simbolos, y por una lei de composición interna que los relaciona. Dita lei de composición interna indica como han d'estar manipulatos os obchectos d'o grupo.
Se diz que un grupo ye abelián u conmutativo cuan berifica amás a propiedat conmutativa:
Notación
editarSe charra de notación aditiva cuan se representa la lei de composición interna como " ", y l'elemento neutro como "0". D'atra man, a notación multiplicativa ye aquella en a que a lei de composición interna se representa como " ", u " ", y l'elemento neutro como "1".
Un segundo eixemplo: grupo de simetría
editarAs simetrias (ye decir, as rotacions y as reflexions) d'un cuadrato forman un grupo dito grupo diedrico, y se denota D4.[7] Tien as siguients simetrías:
- A operación identidat que lo deixa tot tal como yera, denotata id;
- rotacions d'o cuadrato de 90° a la dreita, 180° a la dreita, y 270° a la dreita, denotatas r1, r2 y r3, respectivament;
- reflexions respecto d'os exes vertical y horizontal (fv y fh), u respecto d'as dos diagonals (fd y fc).
Dos simetrías cualsiquiera a y b se pueden composar, ye decir aplicar una dimpués de l'atra. O resultato de fer primero a y dimpués b s'escribe simbolicament d'ezquierda ta dreita como
- b • a ("aplicar a simetría b dimpués d'haber aplicato a simetría a". A notación de dreita ta ezquierda proviene d'a notación ta la composición de funcions).
A tabla de grupo a la dreita presenta os resultatos de totas as composicions posibles. Por eixemplo, chirar 270° a la dreita (r3) y dimpués fer una reflexión horizontal (fh) ye o mesmo que fer una reflexión a lo largo d'a diagonal (fd). Emplegando los simbolos citatos, apareixe en azul en a tabla de grupo:
- fh • r3 = fd.
| • | id | r1 | r2 | r3 | fv | fh | fd | fc |
|---|---|---|---|---|---|---|---|---|
| id | id | r1 | r2 | r3 | fv | fh | fd | fc |
| r1 | r1 | r2 | r3 | id | fc | fd | fv | fh |
| r2 | r2 | r3 | id | r1 | fh | fv | fc | fd |
| r3 | r3 | id | r1 | r2 | fd | fc | fh | fv |
| fv | fv | fd | fh | fc | id | r2 | r1 | r3 |
| fh | fh | fc | fv | fd | r2 | id | r3 | r1 |
| fd | fd | fh | fc | fv | r3 | r1 | id | r2 |
| fc | fc | fv | fd | fh | r1 | r3 | r2 | id |
| Os elementos: id, r1, r2, y r3 forman un subgrupo, se puet veyer en royo (rechión d'a ezquierda superior). Una clase lateral ezquierda y dreita d'iste subgrupo se presenta en berde (en a zaguera ringlera) y amariello (zaguera columna), respectivament. | ||||||||
Datos istos conchuntos de simetrías y a operación descrita, os axiomas de grupo se pueden entender d'a manera siguient:
- 1. L'axioma de clausura necesita que a composición b • a de dos simetrías cualsiquiera a y b sía tamién una simetría. Unatro eixemplo ta la operación de grupo ye
- r3 • fh = fc,
ye decir chirar 270° a la dreita dimpués d'una reflexión horizontal ye igual a una reflexión a lo largo d'a contradiagonal (fc). En efecto cada dos combinacions de dos simetrías dan una simetría, como se puet comprebar fendo servir a tabla de grupo.
- 2. A condición d'asociatividat trata de composar mas de dos simetrías: datos tres elementos a, b y c de D4, bi ha dos maneras posibles de calcular "a allora b allora c". O requisito
- (a • b) • c = a • (b • c)
quiere decir que a composición d'os tres elementos ye independient d'a prioridat d'as operacions, ye decir, composando a con b, y dimpués c con a • b equivale a fer a dimpués d'a composición de b y c. Por eixemplo (fd • fv) • r2 = fd • (fv • r2) como se puet comprebar fendo servir a tabla de grupo d'a dreita
(fd • fv) • r2 = r3 • r2 = r1, que ye igual a fd • (fv • r2) = fd • fh = r1.
- 3. L'elemento identidat ye a simetría id que lo deixa tot inalterato: ta cualsiquier simetría a, realizando id dimpués de a (o a dimpués de id) ye igual a a, de forma simbolica,
- id • a = a,
- a • id = a.
- 4. n elemento inverso desfa la transformación de belatro elemento. Totas as simetrías se pueden esfer: cada una d'as transformacions: id, fh, fv, fd, fc y r2 son a suya propia inversa, porque actuando cadaguna dos vegatas levan o cuadrato a la suya orientación orichinal. As rotacions r3 y r1 son a inversa una de l'atra, porque chirando enta un canto y dimpués o mesmo anglo enta l'atro canto deixa a lo cuadrato inalterato. En simbolos,
- fh • fh = id,
- r3 • r1 = r1 • r3 = id.
A diferencia con o grupo d'enters anterior, a on que l'orden d'a operación ye irrelevant, en D4 sí que importa: fh • r1 = fc pero r1 • fh = fd. En atras parolas, D4 no ye abelián, ixo fa la estructura d'o grupo mas dificil que la d'os enters presentata antis.
Mas eixemplos
editar- , o conchunto de numeros enters con a suma usual, ye un grupo abelián; a on que l'elemento neutro ye o 0, y o simetrico de x, ye -x.
- , o conchunto d'os numeros reals con a suma usual, ye un grupo abelián; a on que l'elemento neutro ye o 0, y o simetrico de x, ye -x.
- , o conchunto d'os numeros reals (escluyendo a lo 0) con a multiplicación, ye un grupo abelián; a on que l'elemento neutro ye l'1, y o simetrico de x ye 1/x. Cal parar cuena que en no tener o cero elemento simetrico multiplicativo, se debe excluyir.
- O conchunto de totas as bicheccions d'un conchunto X - simbolizato por S(X) - chunto con a composición de funcions, ye un grupo no abelián (si a cardinalidat de X ye mayor que dos) y se diz grupo simetrico de X.
- O conchunto de matrices rectangulars de dimensions con a suma, ye un grupo abelián.
- O conchunto de matrices cuadratas con determinant diferent de cero con a multiplicación (Grupo cheneral linial), no ye abelián.
- As clases de homotopía de trachectorias continas en un espacio topolochico X forman un grupo no necesariament abelián. Ista construcción ye o grupo fundamental de X.
- O grupo fundamental d'un cerclo (circle, cercle, Kreis) ye o grupo ciclico infinito; .
- O d'a esfera en ye trivial = 0.
- D'un toro en ye
- D'un toro sin un disco en ye o grupo libre d'orden dos, . D'un toro sin dos discos dischuntos; .
- D'o plan prochectivo en ye
- O d'a botella de Klein en tien a presentación; y que corresponde a lo producto semidreito de con .
Operacions
editarEntre dos grupos G, H puet haber morfismos, por eixemplo funcions que son compatibles con as operacions en cada un d'ellos. Si ye un homomorfismo allora cumple que
a on que emos preso a convención d'escribir ta indicar a operación d'a con b en G, e a operación d' con en H.
O conchunto ye un subgrupo en H cuan S ye un subgrupo en G.
Si transformamos un conmutador: s'otiene: .
Categoría de grupos
editarDende o punto d'envista d'a teoría de categorías, a teoría de grupos poderba catalogar-se como una categoría dita categoría de grupos, debito a que en ella s'estudeya a los grupos y os suyos morfismos. A categoría de grupos ye muit gran, pero puet armar-se una relación de equivalencia en ista categoría ta que se factorice: a relación entre grupos d'estar isomorfos reduce cuestions estructurals d'a categoría de grupos a la categoría de grupos-modulo-los-isomorfos. En ista reducción a operación d'unión dischunta la torna en una categoría monoidal.
Historia
editarAs radices historicas d'a teoría de grupos son a teoría d'as ecuacions alchebraicas, a teoría de numeros y a cheometría. Euler, Gauss, Lagrange, Abel y Galois estioron os investigadors que prencipioron ista ciencia. Galois ye reconoixito como lo primer matematico que relacionó ista teoría con a teoría de cuerpos resultando en a teoría de Galois. Atros importants matematicos en iste campo incluyen a Cayley, Emil Artin, Emmy Noether, Sylow entre muitos atros. Estió Walter von Dick qui en 1882, dió a moderna definición de grupo.
Conceptos basicos
editarTa entender os grupos mas allá d'o nivel de meras manipulacions simbolicas como as d'alto, s'han d'emplegar mas conceptos estructurals.[8] Bi ha un prencipio conceptual subchacent a totas as nocions que siguen: aprofeitar a estructura ofierta por os grupos (que por eixemplo os conchuntos en estar "sin estructura" no tienen) as construccions relacionatas con os grupos han d'estar compatibles con a operación de grupo. Ista compatibilidat se manifiesta en as nocions siguients de diversas maneras. Por eixemplo, os grupos se pueden relacionar la un con l'atro por meyo de funcions ditas homomorfismos de grupo. Por o prencipio debantdito, se desiche que respeten as estructuras de grupo en un sentito preciso. A estructura d'os grupos tamién se puet entender dividindo-los en partis ditas subgrupos y grupos cocient. O prencipio de "conservar estructura" —un tema que se repite muito en matematicas— ye un eixemplo de treballar en una categoría, en iste caso a categoría de grupos.[9]
Homomorfismos de grupo
editarOs homomorfismos de grupo[8] son as funcions que conservan a estructura d'o grupo. Una función a: G → H entre dos grupos ye un homomorfismo si a ecuación: a(g • k) = a(g) • a(k) se cumple ta toz os elementos g, k de G, ye decir o resultato ye o mesmo tanto si se fa la operación de grupo debant como si se fa dimpués d'aplicar a función a. Iste requisito asegura que a(1G) = 1H, y tamién que a(g)−1 = a(g−1) ta tot g de G. Asinas un homomorfismo de grupo respecta tota la estructura de G proporcionata por os axiomas de grupo.[10]
Os grupos G y H se dicen isomorfos si existen homomorfismos de grupo a: G → H y b: H → G, tals que aplicando as dos funcions una dimpués de l'atra (en cada un d'os dos órdens posibles) dan a función identidat de G y H, respectivament. Ye decir, a(b(h)) = h y b(a(g)) = g} ta cualsiquier g de G y h de H. Dimpués d'un punto d'envista abstracto, os grupos isomorfos levan a mesma información. Por eixemplo, contrimostrando que g • g = 1 ta bel elemento g de G ye equivalent a contrimostrar que a(g) • a(g) = 1, porque aplicando a a la primera igualdat da la segunda, y aplicando b a la segunda da atra vegata la primera.
Subgrupos
editarInformalment, un subgrupo ye un grupo H contenito adintro d'un grupo mas gran,[11] Concretament, l'elemento identidat de G ye contenito en H, y siempre que h1 y h2 sían de H, allora tamién lo serán h1 • h2 y h1−1, asinas os elementos d'H, con a operación de grupo en G restrinchita a H, forman un grupo.
En l'eixemplo d'entalto, a identidat y as rotacions constituyen un subgrupo R = {id, r1, r2, r3}, marcato en amariello en a tabla de grupo d'entalto: dos rotacions cualsiquieras composatas son tamién una rotación, y una rotación se puet esfer por (ye decir, ye inversa de) a rotación complementaria 270 ° por 90 °, 180 ° por 180 °, y 90 ° por 270 ° (se veiga que no se define rotación en a dirección oposata). O test de subgrupo ye una condición necesaria y suficient ta que un subconchunto H d'un grupo G sía un subgrupo: ye prou con comprebar que g−1h ∈ H ta toz os elementos g, h ∈ H. Conoixer os subgrupos ye important ta entender o grupo globalment.[12]
Dato cualsiquier subconchunto S d'un grupo G, o subgrupo chenerato por S consta de productos d'elementos de S y os suyos inversos. Iste ye o subgrupo mas chicot de G que contiene S.[13] En l'eixemplo d'entalto, o subgrupo chenerato por r2 y fv consta d'istos dos elementos, l'elemento identidat id y fh = fv • r2. Una atra vegata, ixo ye un subgrupo, porque combinando dos elementos cualsiquiera d'istos cuatre u os suyos inversos (que son, en iste caso particular, istos mesmos elementos) dan un elemento d'iste subgrupo.
Clases laterals
editarEn muitas situacions ye deseyable considerar dos elementos de grupo como si fuesen o mesmo si a suya diferencia perteneixe a un subgrupo dato. Por eixemplo, en D4 definito entalto, una vegata que se realiza una reflexión, o cuadrato nunca no torna a la confeguración de r2 aplicando nomás as operacions de rotación (y no atras reflexions), ye decir as operacions de rotación son irrelevants ta la cuestión de si s'ha realizato una reflexión. As clases laterals se fan servir ta formalizar ista observación: un subgrupo H define clases laterals por a ezquierda u a dreita, que se pueden entender como traslacions de H por un grupo g d'elementos arbitrario. En termins simbolicos, a clase lateral por a ezquierda y por a dreita de H que contienen g son
- gH = {gh, h ∈ H} y Hg = {hg, h ∈ H}, respectivament.[14]
As clases laterals de cualsiquier subgrupo H forman una partición de G; ye decir, por eixemplo, dos clases laterals por a ezquierda u bien son iguals u bien tienen una intersección vueda y a unión de totas as clases laterals por a ezquierda da G.[15] O primer caso (que g1H = g2H) se da precisament cuan g1−1g2 ∈ H, ye decir si a diferencia entre os dos elementos ye un elemento de H. Consideracions similars s'aplican a las clases laterals d'H por a dreita. As clases laterals de H por a ezquierda y por a dreita de H pueden estar iguals u no. Si en son, ye decir ta tot g de G, gH = Hg, se diz que H ye un subgrupo normal. Allora se puet parlar simplament de N como lo conchunto d'as clases laterals.
En D4, o grupo de simetria emplegato en a introducción, as clases laterals por a ezquierda gR d'o subgrupo R que consiste en que as rotacions son u bien iguals a R, si g mesmo ye un elemento de R, u d'atra mán iguals a U = fvR = {fv, fd, fh, fc} (en verde). O subgrupo R tamién ye normal, porque fvR = U = Rfv y de forma parellana ta cualsiquier elemento diferent de fv.
Teoría cheometrica d'os grupos
editarOs mas actuals temas d'investigación en la teoría de grupos tienen que ver con las modernas tecnicas de la topología. Una manera estándard de construir nuevos grupos a partir d'os conoixitos son los
- productos libres,
- productos libres amalgamatos y as
- HNN-extensions.
A gran variedat de tecnicas topolochicas pueden ser aplicatas dende que se sape que ye posible construir siempre un espacio topolochico (de feito un CW-complexo dos-dimensional) de tal manera que o grupo fundamental d'iste espacio ye o grupo dato.
Referencias
editar- ↑ Herstein, 1975 §2, p. 26
- ↑ Hall, 1967 §1.1, p. 1: "The idea of a group is one which pervades the whole of mathematics both pure and applied."
- ↑ En Mathematical Reviews apareixen 3.224 articlos de rechira sobre teoría de grupos y as suyas cheneralizacions escritos en l'anyo l'any 2005
- ↑ Lang, 2005, App. 2, p. 360
- ↑ Herstein, 1975 §2.1, p. 27
- ↑ L'axioma de clausura ya viene implicito por a condición de que • sía una operación. Por ixo bels autors omiten iste axioma. Lang 2002
- ↑ Herstein, 1975 §2.6, p. 54
- ↑ 8,0 8,1 Se veigan, por eixemplo, os libros de Lang (2002, 2005) y Herstein (1996, 1975).
- ↑ Mac Lane 1998
- ↑ Lang 2005, §II.3, p. 34
- ↑ G.Lang 2005, §II.1, p. 19
- ↑ Manimenos, un grupo no ye determinato por o suyo rete de subgrupos. Se veiga Suzuki 1951.
- ↑ Ledermann 1973, §II.12, p. 39
- ↑ Lang 2005, §II.4, p. 41
- ↑ Lang 2002, §I.2, p. 12
Bibliografía
editar- (en) Referencia global en Encyclopaedia of Mathematics
- Alexandroff, P. S.: Introducción a la Teoría de los Grupos, 1967, Buenos Aires, Editorial Universitaria de Buenos Aires, Colección Cuadernos Nº 132.
- Adler, Irving: La Nueva Matemática, 1970, Buenos Aires, Editorial Universitaria de Buenos Aires, Colección Ciencia Joven.